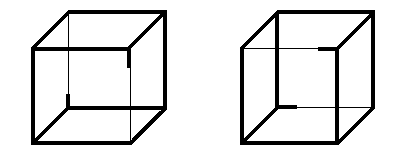
Unmögliche Figuren sind besonders durch die Bilder des holländischen Graphikers Escher bekannt geworden: Wasser fließt im Kreis, aber immer bergauf, Soldaten laufen im Kreis immer die Treppe rauf, in Gebäuden wechselt vorne und hinten.
Eschers Bilder werden oft für optische Täuschungen gehalten, sind es aber nicht.
Es geht nicht darum, zwei gleich lange Strecken unterschiedlich erscheinen zu
lassen o.ä. Escher's Trick besteht darin, dass er Ansichten von rechts und von links (bzw. von oben und von unten) vermischt.

Dadurch entsteht ein ebenes Bild, das wie ein Bild eines dreidimensionalen Gegenstandes aussieht, es aber nicht sein kann. Der menschliche Betrachter deutet es aber so und auf diese Weise entstehen Bilder von unmöglichen Figuren.
Zwei typische unmögliche Grundfiguren:
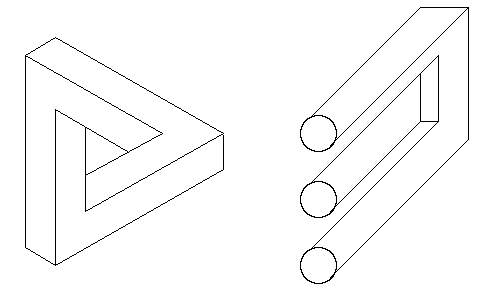
Dies Thema eignet sich ideal für Projekte, in denen Kunst (Perspektive) und Mathematik (Schrägbilder, verdeckte Linien) zusammenarbeiten.
Wer sich mehr für folgende Escher-artige Graphiken interessiert, kann sich den
IFS-Generator von Dirk Surholt laden. Damit kann man nicht nur fraktale
Graphiken erzeugen, sondern eben auch solche Graphiken:
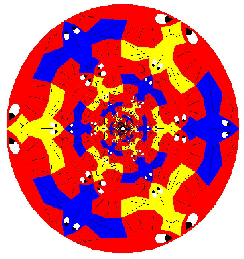
Ebenfalls sehr empfehlenswert ist die CD Escher interactive von DuMont..
© Elschenbroich, Mathe-Werkstatt 03/2001