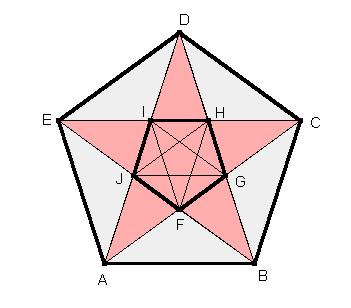
In ein regelmäßiges Fünfeck kann ein Pentagramm eingeschrieben werden, in dem wiederum ein kleineres Fünfeck auftaucht, in das ein Pentagramm einbeschrieben werden kann usw.

Zunächst werden einige Beziehungen zwischen verschiedenen Streckenlängen hergeleitet

Die Dreiecke IHD und IHF sind kongruent, da sie eine gemeinsame Seite und gleiche Winkel haben.

Bezeichnet man die Seitelänge des äußeren Fünfeckes mit a, die des inneren Fünfecks mit a₁ usw., die Schenkellänge des auf das innere Fünfeck aufgesetzten gleichschenkligen Dreiecks mit s₁ usw., so erhält man:
(1)  s₁ = 2·s₂ + a₂ .

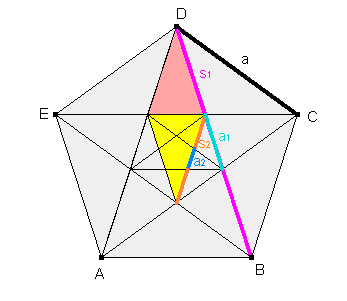
Im Inneren des einbeschriebenen Fünfecks ist ein Parallelogramm zu finden. Dies liefert:
(2)  a₁ = s₂ + a₂.

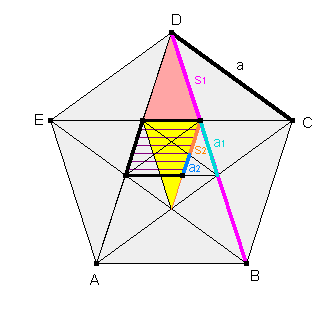
Subtrahiert man die Gleichungen (2) und (1) voneinander, so erhält man:
(3)  s₂ =  s₁ - a₁.

Aus (2)  folgt:  a₂ = a₁ - s₂, Einsetzen von (3) liefert:

(4)  a₂ = 2a₁ - s₁.   

Damit ist jetzt für die nächste einbeschriebene Figur sowohl die Fünfecksseitenlänge als auch die Schenkellänge des aufgesetzten Dreiecks durch Maße der zugehörigen größeren Figur ausgedrückt.

Dieses Vorgehen lässt sich immer wieder durchführen und man erhält:
s₃ =  s₂ - a₂
a₃ = 2a₂ - s₂    usw.   

Nun kommt die Annahme der Kommensurabilität

Wenn wir annehmen, dass im regelmäßigen Fünfeck die Seitenlänge a und die Schenkellänge s des aufgesetzten Dreiecks kommensurabel sind, kann man das Verhältnis s:a als Quotient p:q darstellen, wobei p und q natürliche Zahlen sind und p größer als q ist. Daraus ergibt sich sofort:

(5)  .  Daraus ergibt sich für die nächst kleineren Werte:

(6)     und   .

Wiederholt man dieses Vorgehen, so erhält man als Faktoren von a Brüche mit stets gleichem Nenner q, aber immer kleiner werdenden Zählern. Deswegen lässt sich dies nicht immer wieder durchführen, sondern bricht irgendwann ab. Denn spätestens nach p Schritten wäre man beim Zähler 1 angekommen!

Der entscheidende Schluss

Einerseits ist also klar, dass man das Einbeschreiben immer weiterer Figuren (in Gedanken, über die grenze der Zeichengenauigkeit hinaus) immer weiter durchführen kann.
Andererseits führt die Annahme, dass a und s kommensurabel wären, zu der Folgerung, dass man diesen Vorgang nicht unbegrenzt durchführen könnte.

Dies bedeutet, dass unsere Annahme, s und a wären kommensurabel, nicht zutreffend gewesen sein kann! Der Quotient s/a lässt sich nicht als Verhältnis zweier ganzer Zahlen ausdrücken, ist in unserem heutigen Verständnis also keine Bruchzahl!